Contenido

Introducción

TikZ es un complejo lenguaje gráfico que permite ‘‘dibujar’’ en un documento LaTeX sin ninguna otra herramienta auxiliar.

Para dar nuestros priperos pasos con TikZ, use la siguiente plantilla en $\LaTeX$ para ir probando las distintas alternativas que aquí se presentan.

\documentclass{article}
\usepackage{tikz}
\usetikzlibrary{fit,positioning}
\usepackage{pgfplots}
\pgfplotsset{compat=1.18}
\usepackage{amsmath}

\begin{document}
\pagestyle{empty}

\begin{tikzpicture}
<Tu código aquí>
\end{tikzpicture}

\end{document}

Como se puede ver se cargan los paquetes:

  1. Tikz: \usepackage{tikz} y algunas librerías: \usetikzlibrary{fit,positioning}.
  2. Pgfplots: \usepackage{pgfplots}.

Además, cada vez que queramos crear un dibujo, gráfico o diagrama con TikZ, necesitamos usar el entorno tikzpicture.

TikZ define un conjunto de comandos y entornos $\LaTeX$ para elaborar gráficos de alta calidad. Por ejemplo, el código:

\begin{tikzpicture}
\tikz \draw (0,0) circle (1cm);
\tikz \draw (-1,0) -- (0,1) -- (1,0) -- (0,-1) -- cycle;
\end{tikzpicture}

Genera el siguiente dibujo:

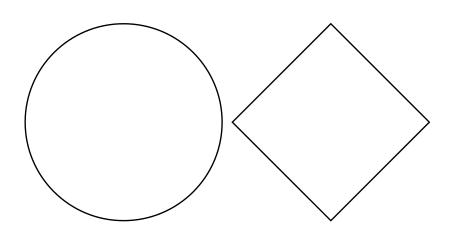
alt text

Las unidades de TikZ, por defecto, son en centímetros. Por lo que la primera linea de código dibuja (con \draw) una circunferencia centrada en el punto (0,0) y radio 1 cm, y en el otro se genera un cuadrado de $\sqrt{2}$ centímetros de lado.

Se observa que el comando \tikz genera dibujos independientes entre sí.
Para que ambos dibujos sean uno solo, generando una figura con el cuadrado y la circunferencia superpuestos, en lugar de usar el comando \tikz, es necesario incluir los comandos de dibujo en un entorno \begin{tikzpicture} sin el comando tikz antes de \draw, por ejemplo:

\begin{tikzpicture}
\draw (0,0) circle (1cm);    
\draw (-1,0) -- (0,1) -- (1,0) -- (0,-1) -- cycle;    
\end{tikzpicture}

Generando la siguiente figura:

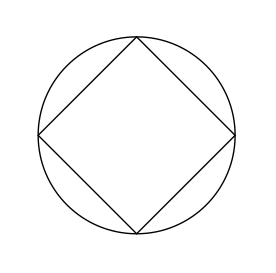
alt text

Las ventajas de usar \tikz en lugar de una herramienta externa son, entre otras:

  1. Control completo sobre la figura, la gráfica o el diagrama.
  2. Se usa el mismo tipo de letra que en el documento.
  3. Capacidad de utilizar macros.
  4. Alta calidad del resultado.

Como inconvenientes:

  1. Elevada curva de aprendizaje (para valientes).
  2. El código puede ser complejo de entender.

A continuación analizaremos algunos comandos útiles para dibujar y graficar en Tikz.

Dibujo básico

Normalmente, un gráfico TikZ se compone utilizando el entorno tikzpicture, como se vio en el ejemplo inicial. Un elemento fundamental en TikZ es el “camino” o “Path”, en inglés. Existen diversos comandos, como \draw, \filldraw o \path que se basan en la idea de encadenar posiciones y unirlas mediante otros elementos (lineas, lineas punteadas, otros).

Analicemos el ejemplo anterior:

\begin{tikzpicture}
\draw (0,0) circle (1cm);    
\draw (-1,0) -- (0,1) -- (1,0) -- (0,-1) -- cycle;    
\end{tikzpicture}
  1. \draw indica que se debe “dibujar” el camino a realizar. Cada comando \draw inicia un nuevo camino.
  2. El camino se expresa por una sucesión de puntos y “operaciones” que expresan lo que hay que hacer entre cada punto.
  3. En la linea 1 con el comando draw, la operación “circle” indica que se debe dibujar una circunferencia de centro $(0,0)$ y radio $1cm$.
  4. Con el comando draw, la operación -- indica que se debe dibujar una línea recta entre el punto anterior y el siguiente.
  5. (-1,0) -- (0,1) indica que se debe posicionar en el punto $(-1,0)$ y se debe dibujar una recta hacia el punto $(0,1)$ y así sucesivamente. En centímetros por defecto.
  6. “cycle” indica que se vaya al punto de inicio del camino actual.

Existen diversas operaciones para recorrer un camino: rectangle, grid, ellipse, son algunas de las factibles. Cada una de ellas necesita unos parámetros determinados para su correcto dibujo (googlear cada uno).

Otras formas

Uno de los comandos más simples y comúnmente utilizados en TikZ es el comando \draw. Veamos algúnos de sus usos.

  1. Para dibujar una línea recta: Ingresamos una coordenada de inicio $(a,b)$, seguida de dos guiones -- antes de la coordenada de finalización. Luego, terminamos la declaración cerrándola con un punto y coma ;. 
    \begin{tikzpicture}
\draw (0,0) -- (4,0);
\end{tikzpicture}

    alt text

  2. Para dibujar un cuadrado: Ingresamos todas las coordenadas de los vértices, seguida de dos guiones -- antes de la coordenada de finalización. Luego, terminamos la declaración cerrándola con un punto y coma ;. 
    \begin{tikzpicture}
\draw (0,0) -- (4,0) -- (4,4) -- (0,4) -- (0,0);
\end{tikzpicture}

    ó

    \begin{tikzpicture}
\draw (0,0) -- (4,0) -- (4,4) -- (0,4) -- cycle;
\end{tikzpicture}

    Para simplificar aún más este código, podemos usar la palabra clave rectangle después de la coordenada de inicio y luego seguir con la coordenada de la esquina diagonalmente opuesta.

    \begin{tikzpicture}
\draw (0,0) rectangle (4,4);
\end{tikzpicture}

    alt text

  3. También podemos agregar líneas que no son rectas. Por ejemplo, para dibujar una parábola usamos: 
    \begin{tikzpicture}
\draw (0,0) parabola (4,4);
\end{tikzpicture}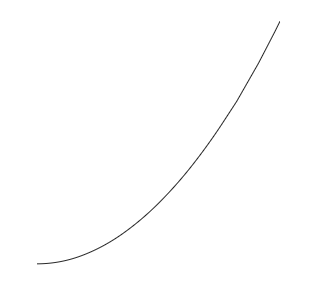

    Parábola

  4. Para agregar una línea curva, usamos puntos de control. Comenzamos con nuestra coordenada de inicio, luego usamos dos puntos .. seguidos de la palabra clave controls y luego las coordenadas de nuestros puntos de control separadas por un and. Luego, después de dos puntos .. más, tenemos el punto final. Estos puntos de control actúan como imanes que atraen la línea en su dirección: 
    \begin{tikzpicture}
\draw (0,0) .. controls (4,0) and (0,4) .. (4,4);
\end{tikzpicture}

    Puntos de control

  5. Para dibujar una circunferencia: La primera coordenada es el centro de la circunferencia y la longitud entre paréntesis al final es su radio. 
    \begin{tikzpicture}
\draw (2,2) circle (3cm);
\end{tikzpicture}

    Circulo

  6. Para dibujar una elipse. Esta vez, las longitudes entre paréntesis, separadas por un and, son el eje mayor en la dirección $x$ y el eje menor en la dirección $y$, respectivamente. La coordenada $(2,1)$ es el centro de la elipse: 
    \begin{tikzpicture}
\draw (2,1) ellipse (3cm and 1cm);
\end{tikzpicture}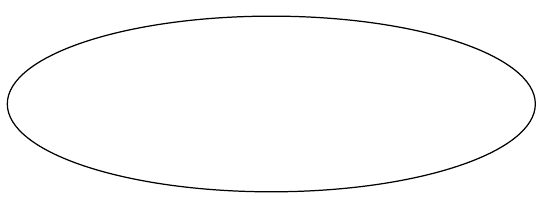

    Elipse

  7. Para dibujar un arco. El parentesis inicial es el centro $(1,1)$ y en el paréntesis final ingresamos el ángulo de inicio, el ángulo de finalización y el radio. Esta vez estos valores están separados por dos puntos :. 
    \begin{tikzpicture}
\draw (2,1) arc (0:130:3cm);
\end{tikzpicture}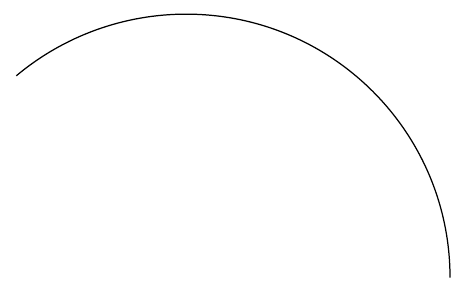

    Arco
    Para personalizar la forma en que se dibujan estas líneas, agregamos argumentos adicionales al comando \draw. Por ejemplo, podemos editar la circunferencia que dibujamos para que la línea sea roja, gruesa y punteada o en el cuadrado para que la linea sea verde, gruesa y punteada:

    \begin{tikzpicture}
\draw[red,thick,dashed] (0,1) circle (2cm);
\draw[green,thick,dashed] (0,-1) rectangle (4,3);
\end{tikzpicture}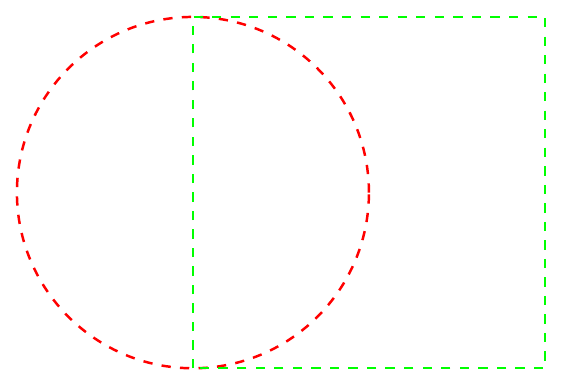

    Circunferencia y cuadrado

  8. Para dibujar un mallado: Usamos el comando \draw seguido de algunos argumentos adicionales. 
    \begin{tikzpicture}
\draw[step=1cm,gray,very thin] (-1,-1) grid (5,5);
\end{tikzpicture}

    Por ejemplo, especificamos el tamaño del paso de la cuadrícula usando step= y una longitud. También hemos especificado el color gris y le hemos dicho que haga las líneas muy delgadas. Después de estos argumentos, ingresamos las coordenadas de la esquina inferior izquierda, seguidas de la palabra clave grid y luego las coordenadas de la esquina superior derecha.
    Con contorno
    o sin contorno

    \begin{tikzpicture}
\draw[step=1cm,gray,very thin] (-0.9,-0.9) grid (4.9,4.9);
\end{tikzpicture}

    Sin contorno

Estilos

Los diferentes comandos tienen parámetros opcionales que facilitan el diseño de diferentes estilos para los gráficos. Por ejemplo:

  1. Para colorear, usamos el comando \fill en lugar del comando \draw. Luego, entre corchetes, ingresamos un color (40% azul mezclado con 60% blanco). Después, simplemente especificamos una forma cerrada (circunferencia, rectángulo, elipse, otra) como lo haríamos normalmente. 
    \begin{tikzpicture}
\draw[step=1cm,gray,very thin] (-1,-1) grid (5,5);
\fill[blue!40!white] (2,2) circle (2);
\end{tikzpicture}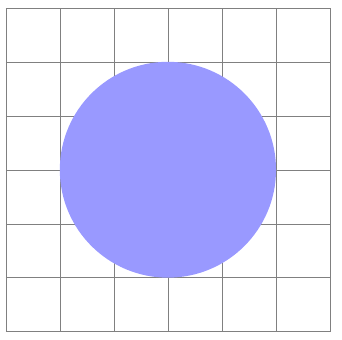

    Circulo

  2. Si quisiéramos agregar un borde alrededor de esta figura, debemos usar el comando \filldraw y luego modificar los argumentos para tener tanto un color de relleno como un color de contorno especificado: 
    \begin{tikzpicture}
\draw[step=1cm,gray,very thin] (-1,-1) grid (5,5);
\filldraw[fill=blue!40!white, draw=black] (0,0) rectangle (4,4);
\end{tikzpicture}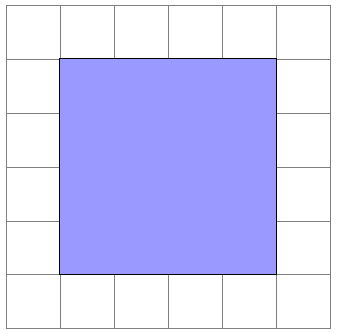

    Cuadrado

Analicemos el siguiente código:

\begin{tikzpicture}
\draw[step=0.5,color=red!50!white, very thin] (-1.5,-1.5) grid (1.5,1.5);
\draw (-2,0) -- (2,0);
\draw (0,-2) -- (0,2);
\draw[thick, color=blue] (-2,1.5) .. controls (0,-2) .. (2,1.5);
\filldraw[color=gray] (-2,1.5) circle (3pt);
\filldraw[color=gray] (2,1.5) circle (3pt);
\filldraw[color=gray] (0,-2) circle (3pt);
\end{tikzpicture}

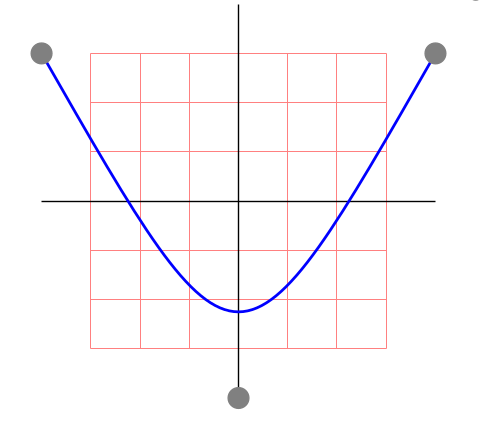
alt text

Se observa que:

  1. El primer comando tiene unos parámetros envueltos entre corchetes. Estos parámetros permiten matizar el funcionamiento de las operaciones a realizar en el comando. En concreto, están indicando:
    • step que al dibujar el mallado con grid, la malla tenga un grosor de medio centímetro.
    • color, expresa, en formato xcolor, que debe dibujar en color rojo claro.
    • very thin, expresa el grosor de las líneas que se dibujen en este comando, en este caso concreto, la malla a pintar.
  2. Los dos siguientes comandos \draw dibujan los ejes horizontales con el estilo por defecto (líneas negras de grosor thin).
  3. El siguiente comando \draw dibuja una línea desde el punto (-2,1.5) al punto (2,1.5), pero en lugar de ser recta, la operación .. controls (0,-2) .., establece que se dibuje la línea utilizando este punto de control como elemento de referencia para trazarla curva. Lo que hace tikz es “salir” del punto inicial de forma paralela a la recta imaginaria que llegaría al punto de control, para después girar de tal modo que llegue al punto de destino de forma paralela a la recta imaginaria que va del punto de destino al punto de control. La sintaxis de esta operación permite utilizar dos puntos de control diferentes para el origen y el destino, así tanto el ángulo como la distancia a dichos puntos definen la forma de la curva a trazar. En este comando también se ha especificado un estilo entre corchetes, línea gruesa y de color azul.
  4. Los tres últimos comandos \filldraw dibujan con relleno: se posicionan en un punto; después, la operación a ejecutar es circle, con un radio de 3pt, que en este caso se rellenan del mismo color que se ha indicado, gray, gris.

Con estas herramientas se pueden realizar dibujos muy complejos. Para facilitar al máximo su desarrollo, tikz permite, además, darle nombre a los estilos y reutilizarlos tantas veces como se necesite. Por ejemplo, el dibujo anterior se puede reescribir de la siguiente forma:

\begin{tikzpicture}[
migrid/.style ={step=0.5,color=red!50!white, very thin},
micurva/.style ={thick, color=blue},
mipunto/.style ={color=gray}]
\draw[migrid] (-1.5,-1.5) grid (1.5,1.5);
\draw (-2,0) -- (2,0);
\draw (0,-2) -- (0,2);
\draw[micurva] (-2,1.5) .. controls (0,-2) .. (2,1.5);
\filldraw[mipunto] (-2,1.5) circle (3pt); 
\filldraw[mipunto] (2,1.5) circle (3pt); 
\filldraw[mipunto] (0,-2) circle (3pt); 
\end{tikzpicture}
  1. migrid/.style define un estilo de nombre migrid que se puede utilizar entre corchetes en los diferentes comandos para aplicar los parámetros que definen el estilo.
  2. Después del signo =, entre llaves, se describen los parámetros que definen el estilo. Esto permite la reutilización como se observa en los tres comandos \filldraw.

Ejes y gráficas de funciones

Ejes:

A continuación veremos como agregar ejes etiquetados (etiquetas) a nuestra cuadrícula. Para hacer esto, dibujamos dos líneas normales, ambas desde $(0,0)$, pero las haremos gruesas y agregaremos cabezas de flecha usando un guion y un corchete puntiagudo ->:

\begin{tikzpicture}
\draw[step=1cm,gray,very thin] (-0.1,-0.1) grid (5.6,5.6);
\draw[thick,->] (0,0) -- (5.5,0);
\draw[thick,->] (0,0) -- (0,5.5);
\end{tikzpicture}

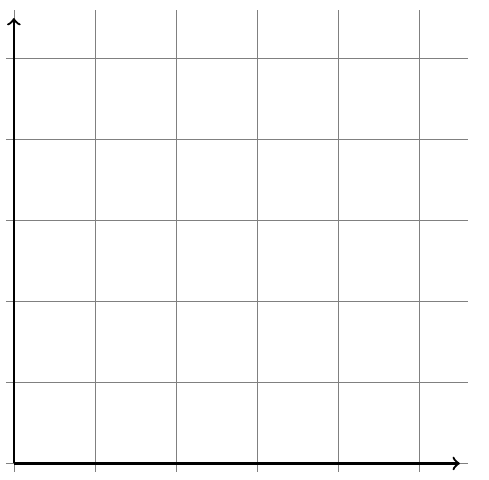
Ejes cartesianos

También podemos etiquetar nuestros ejes usando nodos. Para hacer esto, agregamos la palabra clave node en ambos enunciados \draw junto a las coordenadas de finalización, seguido de una especificación de anclaje entre corchetes cuadrados y el texto entre llaves. Cada nodo que creamos en TikZ tiene varios anclajes. Entonces, cuando especificamos el anclaje north west para el nodo del eje $x$, le estamos diciendo a TikZ que use el anclaje en la esquina superior izquierda para anclar el nodo a la coordenada.

\begin{tikzpicture}
\draw[step=1cm,gray,very thin] (-0.1,-0.1) grid (5.6,5.6);
\draw[thick,->] (0,0) -- (5.5,0) node[anchor=north west] {$x$};
\draw[thick,->] (0,0) -- (0,5.5) node[anchor=south east] {$y$};
\draw (2,2) node {Estoy aquí};
\draw node at (4.5,4.5) {$\displaystyle\int f d\mu$};
\draw node at (4.5,3.5) {$f(x) = \sin(x)$};
\draw node at (1.5,1.5) {$|e^{i\theta}|=1$};
\end{tikzpicture}

Node
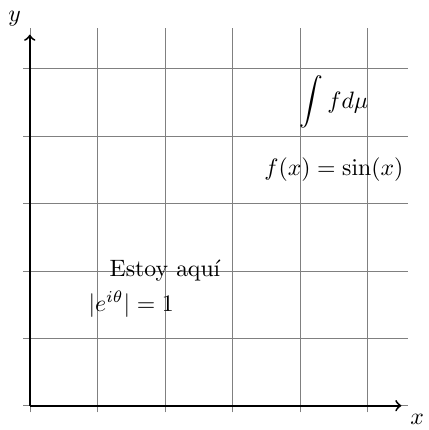
Note las diferentes formas de usar el comando node en el código anterior. Se puede agregar información sobre la imagen usando este comando, hemos agregado el texto $\displaystyle\int f d\mu$ en la coordenada $(4.5,4.5)$.
También podemos agregar marcas y numeración sobre los ejes de la siguiente manera:

\begin{tikzpicture}
\draw[step=1,gray,very thin] (-0.1,-0.1) grid (5.6,5.6);
\draw[thick,->] (0,0) -- (5.5,0) node[anchor=north west] {$x$};
\draw[thick,->] (0,0) -- (0,5.5) node[anchor=south east] {$y$};
\foreach \x in {0,1,2,3,4,5}
   \draw (\x,1pt) -- (\x,-1pt) node[anchor=north] {$\x$};
\foreach \y in {0,1,2,3,4,5}
    \draw (1pt,\y) -- (-1pt,\y) node[anchor=east] {$\y$};
\end{tikzpicture}

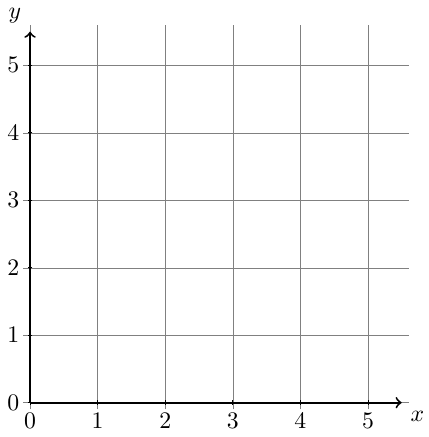
Ejes con etiquetas
El código utiliza dos bucles \foreach para recorrer sistemáticamente los ejes agregando las marcas y los números. En cada uno, la variable $x$ o $y$ toma todos los números entre las llaves {...}, uno a uno, y ejecuta el comando \draw.

Gráficas de funciones:

En TikZ se pueden generar gráficas de funciones de alta calidad como el que sigue:

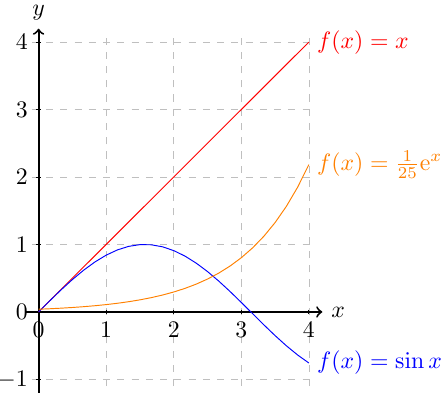
alt text
El código es el que sigue:

\begin{tikzpicture}[domain=0:4]
\draw[very thin,color=lightgray,dashed] (-0.1,-1.1) grid (4.1,4.1);
\draw[thick,->] (-0.2,0) -- (4.2,0) node[right] {$x$};
\draw[thick,->] (0,-1.2) -- (0,4.2) node[above] {$y$};
\foreach \x in {0,1,2,3,4}
   \draw (\x,1pt) -- (\x,-1pt) node[anchor=north] {$\x$};
\foreach \y in {-1,0,1,2,3,4}
    \draw (1pt,\y) -- (-1pt,\y) node[anchor=east] {$\y$};
\draw[color=red] plot(\x,{\x}) node[right] {$f(x) =x$};
\draw[color=blue] plot(\x,{sin(\x r)}) node[right] {$f(x) = \sin x$};
% El r que aparece en el argumento de la función indica que se evaluara la función en radianes.
\draw[color=orange,variable=\t] plot(\t,{(1/25)*exp(\t)}) node[right] {$f(x) = \frac{1}{25} \mathrm e^x$};
\end{tikzpicture}

Cuando se grafica una función, las coordenadas de los datos de la gráfica se pueden calcular evaluando una expresión matemática. Dado que pgf incluye un motor matemático, puedes especificar esta expresión y luego hacer que TikZ produzca automáticamente las coordenadas deseadas.

La sintaxis es sencilla: Después del comando plot y sus opciones locales, se proporciona directamente una ⟨expresión de coordenada⟩, en el ejemplo anterior (\x,{sin(\x r)}). Parece una coordenada normal, pero dentro de ella puedes usar una macro especial, que es \x por defecto, aunque esto se puede cambiar utilizando la opción variable (como en la linea 10 del código anterior). La ⟨expresión de coordenada⟩ se evalúa para diferentes valores de \x y las coordenadas resultantes se grafican.

Ten en cuenta que a menudo tendrás que poner la coordenada $x$ o $y$ entre llaves, especialmente cuando usas una expresión que implique paréntesis.
Las siguientes opciones influyen en cómo se evalúa la ⟨expresión de coordenada⟩:

  1. variable=⟨macro⟩: Establece la macro cuyo valor se asigna a los diferentes valores cuando se evalúa la ⟨expresión de coordenada⟩ (sin valor predeterminado, inicialmente \x).
  2. samples=⟨número⟩: Establece el número de muestras utilizadas en la gráfica (sin valor predeterminado, inicialmente samples=25).
  3. domain=⟨inicio⟩:⟨fin⟩: Establece el dominio del cual se debe evaluar la variable (sin valor predeterminado, inicialmente domain=-5:5).
  4. samples at=⟨lista de muestras⟩: Esta opción especifica una lista de posiciones para las cuales se debe evaluar la variable. Por ejemplo, puedes decir samples at={1,2,8,9,10} para que la variable se evalúe exactamente para los valores $1$, $2$, $8$, $9$ y $10$. Puedes usar la sintaxis \foreach, por lo que puedes usar ... dentro de la ⟨lista de muestras⟩.
    Cuando se usa esta opción, las opciones samples y domain quedan anuladas. A la inversa, configurar samples o domain anulará esta opción.

Una gráfica levemente mas interesante se puede conseguir de la siguiente manera:

\begin{tikzpicture}
% Definición de variables
\def\xa{-pi-0.3}
\def\xb{pi+0.4}
\def\ya{-3.4}
\def\yb{ 3.6}
\def\ea{0.28}
\def\eb{0.26}
\def\N{100} % numero de puntos
% Ejes y mallado
\draw[xstep=pi/2, very thin, color=lightgray, dashed] (\xa,\ya) grid (\xb,\yb);
\draw[thick,->] (\xa,0) -- (\xb,0) node[right] {$x$}; % eje X
\draw[thick,->] (0,\ya) -- (0,\yb) node[left] {$y$}; % eje Y
% Ticks para eje x
\foreach \x in {-pi,-pi/2,0,pi/2,pi}
    \draw[thick] (\x,2pt) -- (\x,-2pt);
\draw % x
  node[below,scale=0.9] at (-pi,0) {$-\pi$}
  node[below,scale=0.9] at (-pi/2,0) {$-\frac{\pi}{2}$}
  node[below,scale=0.9] at (0,0) {$0$}
  node[below,scale=0.9] at (pi/2,0) {$\frac{\pi}{2}$}
  node[below,scale=0.9] at (pi,0) {$\pi$};
% Ticks para eje y
\foreach \y in {-3,-2,-1,0,1,2,3}
    \draw[thick] (2pt,\y) -- (-2pt,\y) node[anchor=east] {$\y$};
% functions
\draw[color=blue,samples=\N,domain=\xa:\xb] % función seno
  plot(\x,{sin(\x r)}) % r for radians
  node[above right] at (pi/2,1) {$f(x)=\sin(x)$};
\draw[color=red,samples=\N,domain=\xa:\xb] % función coseno
  plot(\x,{cos(\x r)})
  node[above left] at (-pi/2+0.5,-2) {$g(x)=\cos(x)$};
\draw[color=orange] % función tangente
  plot[samples=\N,domain=\xa:-pi/2-\eb] (\x, {tan(\x r)})
  plot[samples=\N,domain=-pi/2+\ea:pi/2-\eb] (\x, {tan(\x r)})
  plot[samples=\N,domain=pi/2+\ea:pi-\eb] (\x, {tan(\x r)})
  node[above right] at (pi/2,3.0) {$h(x)=\tan(x)$};
\end{tikzpicture}

El código anterior genera la siguiente gŕafica:
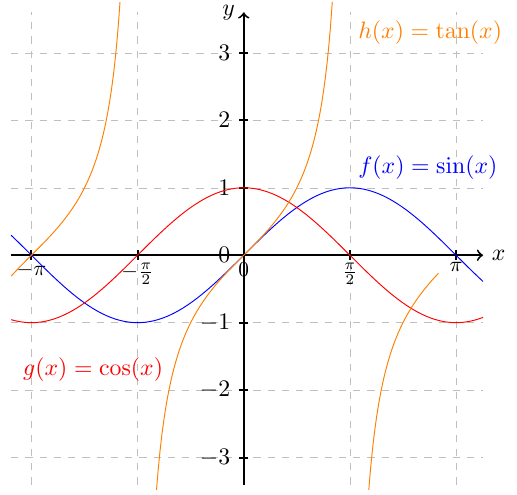
Función seno coseno tangente

El código anterior tiene algunos ingredientes nuevos.

  1. \def define variables en latex, aquí se definen algunas variables que se usarán mas adelante, entre ellas: Los límites de los ejes $x$ (\xa{-pi-0.3} y \xb{pi+0.4}) e $y$ (\ya{-3.4} y \yb{ 3.6}), respectivamente y \N como el número de samples.
  2. El siguiente segmento de código 
    \draw % x
node[below,scale=0.9] at (-pi,0) {$-\pi$}
node[below,scale=0.9] at (-pi/2,0) {$-\frac{\pi}{2}$}
node[below,scale=0.9] at (0,0) {$0$}
node[below,scale=0.9] at (pi/2,0) {$\frac{\pi}{2}$}
node[below,scale=0.9] at (pi,0) {$\pi$};

    genera manualmente las etiquetas sobre el eje $x$ en formato latex.

Funciones soportadas

A continuación se presenta una lista de las funciones que soporta TikZ.

abs cosh frac ln notless sec
acos cot gcd log10 oct sign
add deg greater log2 or sin
and depth height max pi sinh
array dim hex min pow sqrt
asin div Hex mod rad subtract
atan divide int Mod rand tan
atan2 e ifthenelse multiply random tanh
bin equal iseven neg real true
ceil factorial isodd not rnd veclen
cos false isprime notequal round width
cosec floor less notgreater scalar  

donde,

Función Descripción Función Descripción
abs valor absoluto acos arcocoseno
add sumar and y lógico
array matriz asin arcoseno
atan arcotangente atan2 arcotangente de dos parámetros
bin binario ceil techo (parte entera superior)
cos coseno cosec cosecante
cosh coseno hiperbólico cot cotangente
deg grados depth profundidad
dim dimensión div dividir
e constante e equal igual
factorial factorial false falso
floor piso (parte entera inferior) frac fracción
gcd máximo común divisor greater mayor
height altura hex hexadecimal
int entero ifthenelse si entonces sino
iseven es par isodd es impar
isprime es primo less menos
ln logaritmo natural log10 logaritmo base 10
log2 logaritmo base 2 max máximo
min mínimo mod módulo
Mod módulo (otra forma) multiply multiplicar
neg negativo not no lógico
notequal no igual notgreater no mayor
notless no menor oct octal
or o lógico pi pi
pow potencia rad radianes
rand aleatorio random aleatorio
real real rnd aleatorio (otra forma)
round redondear scalar escalar
sec secante sign signo
sin seno sinh seno hiperbólico
sqrt raíz cuadrada subtract restar
tan tangente tanh tangente hiperbólica
true verdadero veclen longitud de vector
width ancho    

Gráficos de barras

Para diagramas más avanzados, como por ejemplo, un diagrama de barras, se puede utilizar el paquete pgfplots que se basa en pgf/tikz y simplifica su construcción. Para ello es necesario incluir en el preámbulo: \usepackage{pgfplots}, que añade la librería pgfplots. Por ejemplo:

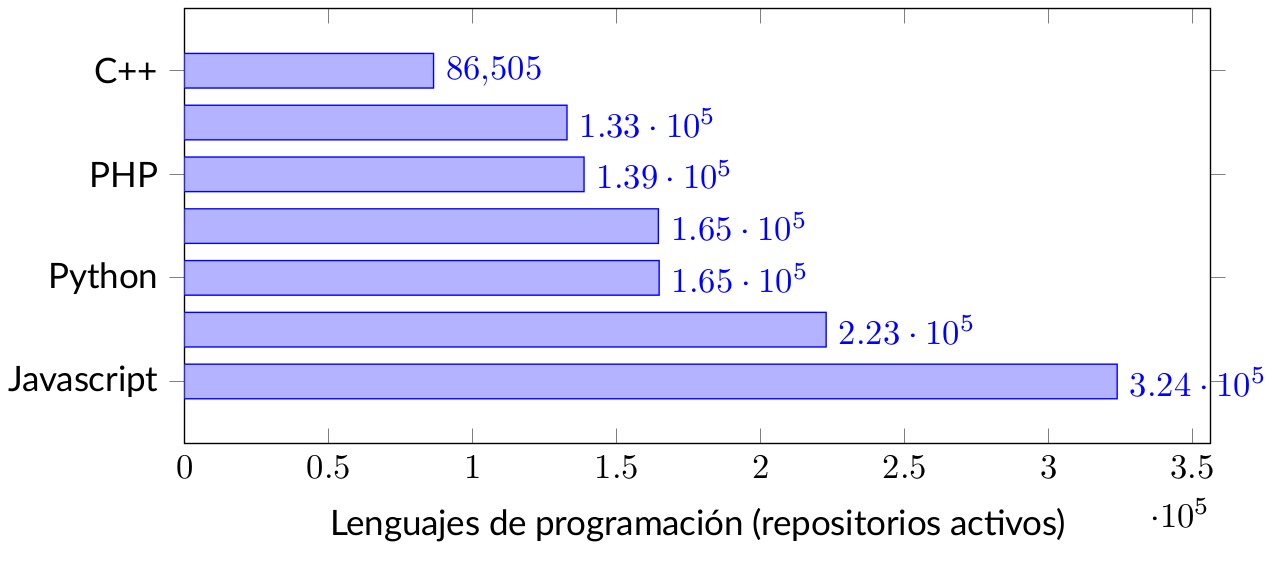alt text Se obtiene con este código:

\begin{tikzpicture}[scale=0.85]
\begin{axis}[
xbar, xmin=0,
width=12cm, height=6cm, enlarge y limits=0.2,
xlabel={Lenguajes de programación (repositorios activos)},
symbolic y coords={Javascript, Java, Python, CSS, PHP, Ruby, C++},
nodes near coords, nodes near coords align={horizontal},
]
\addplot coordinates {(323928,Javascript)
(222852,Java)
(164852,Python)
(164585,CSS)
(138771,PHP)
(132848,Ruby)
(86505,C++)};
\end{axis}
\end{tikzpicture}

Nodos

Los nodos facilitan la generación de diagramas que contengan textos o que requieran mostrar relaciones entre elementos, entre otras cosas.
A continuación se muestra un ejemplo de uso de los nodos que utiliza algunas librerías adicionales para facilitar su diseño.

  1. fit, para calcular el tamaño de los nodos.
  2. positioning, para colocar los nodos en posiciones relativas a otros.
    Para utilizar estas librerías auxiliares de TikZ se utiliza el comando: \usetikzlibrary{fit,positioning}.
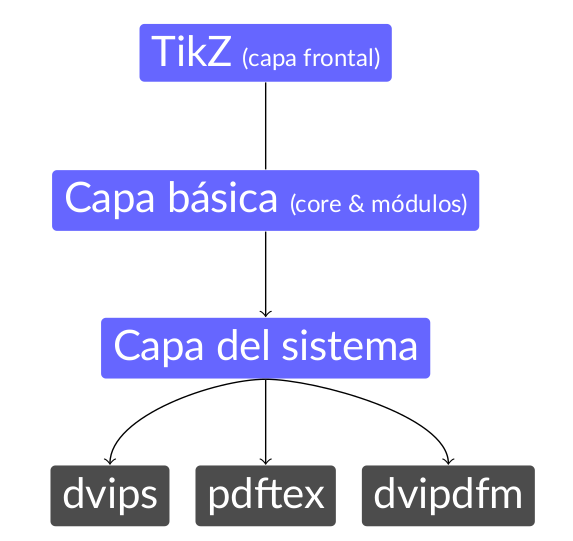
    alt text
\begin{tikzpicture}[node distance= 1.5cm, auto,
every node/.style={text=white, rounded corners=0.05cm},
grande/.style={rectangle,  fill=blue!60!white, font=\large}, 
peque/.style={rectangle, fill=white!30!black, font=\large}]

\node[grande](sistema){Capa del sistema};
\node[grande, above of=sistema](basico){Capa básica \scriptsize (core \& módulos)};
\node[grande, above of=basico](tikz){TikZ \scriptsize (capa frontal)};
\node[peque, below of=sistema](pdftex){pdftex};
\node[peque, left=0.25cm of pdftex](dvips){dvips};
\node[peque, right=0.25cm of pdftex](dvipdfm){dvipdfm};

\draw[->] (tikz.south) -- (basico.north) (basico.south) -- (sistema.north);
\draw[->] (sistema.south) .. controls +(left:0.5cm) and +(up:0.5cm) .. (dvips.north);
\draw[->] (sistema.south) .. controls +(right:0.5cm) and +(up:0.5cm) .. (dvipdfm.north);
\draw[->] (sistema.south) -- (pdftex.north);
\end{tikzpicture}

Se observa que:

  1. Las primeras líneas establecen los estilos a utilizar: El texto será de color blanco para todos los nodos y las esquinas redondeadas; los nodos con el estilo “grande” utilizan un color de relleno diferente a los pequeños, el tipo de letra será grande y deberán tener forma de “rectangle”.
  2. En cada comando \node se observa, entre paréntesis, el “nombre” que tendrá el nodo, seguido de su contenido entre llaves. El “nombre” se utiliza para referenciar al nodo desde otro lugar. En este caso concreto, para establecer la posición relativa entre ellos.
  3. Entre los parámetros de cada nodo se incluye el estilo y la posición relativa a otro nodo: above of, below of, left y right. Se observa que se puede incluir la distancia relativa de separación entre ellos.
  4. Para dibujar las líneas que conectan los nodos, se utiliza draw. El parámetro especifica el tipo de línea a dibujar, en este caso con una flecha al final (pero no al comienzo) del camino.
  5. Si se desease una línea con flecha tanto al comienzo como al final del camino se debería utilizar <->. Para expresar una flecha solo al comienzo, se utilizar <-.
  6. Para indicar los lugares de origen y de destino de la línea, se indican los nombres de los respectivos nodos, seguidos de un punto y del modificador que expresa el punto del que debe salir: north, desde el borde superior; south, desde el inferior; east, desde el borde derecho, y west, desde el borde izquierdo. Si no se indican los puntos de inicio y fin de la línea, TikZ busca los más próximos entre sí.
  7. Para expresar una línea curva se utiliza controls como se vio anteriormente. En este caso se indican dos puntos de control. Ambos, precedidos del símbolo +, que sirve para expresar coordenadas relativas, a los puntos de salida y llegada respectivamente.
  8. Cada punto de control, además de ser relativo, indica posición, no mediante un punto $(x,y)$ sino mediante un desplazamiento a través de un eje. Este se expresa con el texto left o right, en este caso.

TikZ es tan potente que permite expresar el mismo dibujo de diversas maneras. En este caso se puede hacer uso de la operación edge que facilita la unión entre nodos, sin necesidad de indicar draw. De este modo se captura la semántica entre nodos y enlaces. El codigo queda así:

\begin{tikzpicture}[node distance= 1.5cm, auto,
every node/.style={text=white, rounded corners=0.05cm},
grande/.style={rectangle,  fill=blue!60!white, font=\large}, 
peque/.style={rectangle, fill=white!30!black, font=\large}]

\node[grande](sistema){Capa del sistema}
edge[->, bend right=20] (dvips)
edge[->] (pdftex)
edge[->, bend left=20] (dvipdfm);
\node[grande, above of=sistema](basico){Capa básica \scriptsize (core \& módulos)}
edge[->] (sistema);
\node[grande, above of=basico](tikz){TikZ \scriptsize (capa frontal)}
edge[->] (basico);
\node[peque, below of=sistema](pdftex){pdftex};
\node[peque, left=0.25cm of pdftex](dvips){dvips};
\node[peque, right=0.25cm of pdftex](dvipdfm){dvipdfm};    
\end{tikzpicture}

Como se observa, la operación edge, en el comando \node, facilita el dibujo del enlace entre el nodo que se está definiendo y otro que se indica por su nombre. Además, es posible expresar el “grado de curvatura” del enlace y TikZ se encargará de posicionar la curva en el mejor lugar posible.

Referencias

  1. Página del proyecto TikZ en CTAN.
  2. Introducción simple a TikZ: A very minimal introduction to TikZ.
  3. Muchos ejemplos de TikZ y PGF: TikZ and PGF examples.
  4. Página del paquete pgfplots.

Al finalizar

En caso de identificar errores en la documentación, en la resolución, implementación u otro, o si quieres proponer una solución más elegante a las problemáticas propuestas, escríbeme a vosores@ucm.cl